Unit 7 homework 2 special right triangles – Embark on a mathematical journey with Unit 7 Homework 2: Special Right Triangles, where we delve into the fascinating world of triangles with unique properties. From their defining characteristics to their practical applications, this exploration promises to illuminate the intricacies of these geometric marvels.
As we unravel the secrets of special right triangles, we will uncover the Pythagorean theorem’s profound connection to their side lengths. Through captivating examples and insightful discussions, we will witness the power of these triangles in solving real-world problems. Prepare to be enthralled as we explore the depths of geometry, unlocking the hidden potential of special right triangles.
1. Define Special Right Triangles
Special right triangles are triangles with specific angle measures that result in unique side length relationships. These triangles have specific properties that make them useful in various applications.
Characteristics of special right triangles include:
- One right angle (90 degrees)
- Specific ratios between the side lengths
- Commonly used in geometry, trigonometry, and practical applications
Examples of special right triangles include:
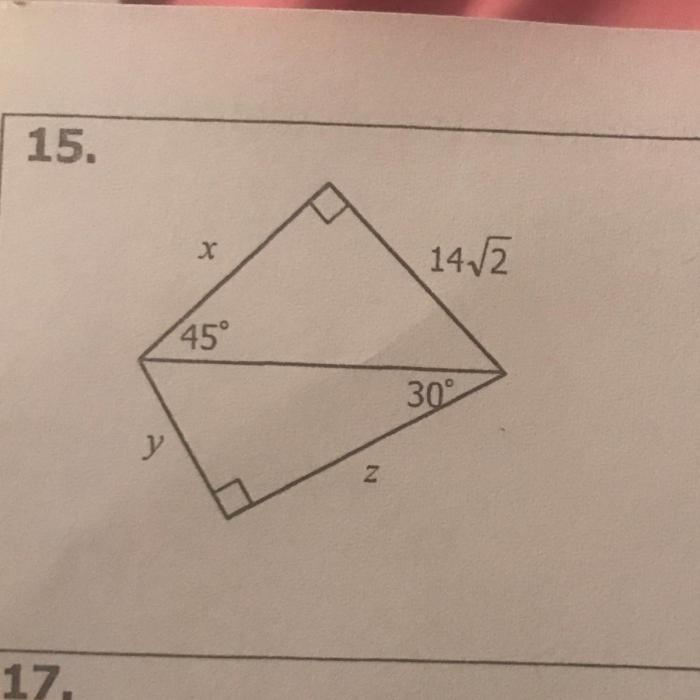
- 45-45-90 triangle: All angles are 45 degrees, and the side lengths have a ratio of 1:1:√2.
- 30-60-90 triangle: One angle is 30 degrees, one angle is 60 degrees, and the side lengths have a ratio of 1:√3:2.
2. Pythagorean Theorem and Special Right Triangles
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
For special right triangles, the Pythagorean theorem can be used to find missing side lengths. For example, in a 45-45-90 triangle, if one leg has a length of 3, then the other leg and the hypotenuse can be found using the Pythagorean theorem:
- Leg 2: √(3 2+ 3 2) = √(18) = 3√2
- Hypotenuse: √(3 2+ 3√2 2) = √(27 + 18) = 3√3
The following table compares the side ratios of different special right triangles:
| Triangle | Angle Measures | Side Ratios |
|---|---|---|
| 45-45-90 | 45°, 45°, 90° | 1:1:√2 |
| 30-60-90 | 30°, 60°, 90° | 1:√3:2 |
3. Applications of Special Right Triangles
Special right triangles are used in various real-world applications, including:
- Architecture:Designing roofs, stairs, and other structures that require precise angles and measurements.
- Engineering:Calculating forces, moments, and stresses in structures such as bridges and buildings.
- Surveying:Measuring distances and angles in land surveying and mapping.
- Navigation:Determining the direction and distance traveled using trigonometry and special right triangles.
For example, in architecture, the 45-45-90 triangle is used to design roofs with equal-length rafters. The 30-60-90 triangle is used to calculate the height of a building or the length of a shadow.
4. Properties of Special Right Triangles
Different types of special right triangles have specific properties:
- 45-45-90 triangles:
- Congruent legs
- Hypotenuse length is √2 times the length of each leg
- 30-60-90 triangles:
- One leg is half the length of the hypotenuse
- The other leg is √3 times half the length of the hypotenuse
These properties can be used to solve problems involving special right triangles. For example, if you know the length of one leg of a 30-60-90 triangle, you can use the properties to find the lengths of the other two sides.
5. Advanced Concepts
Advanced concepts related to special right triangles include:
- Trigonometry:Using the trigonometric functions (sine, cosine, and tangent) to find angles and side lengths in special right triangles.
- Geometry:Applying geometric principles, such as the Pythagorean theorem and similarity, to analyze and solve problems involving special right triangles.
These concepts can be used to further analyze special right triangles and solve complex problems. For example, trigonometry can be used to find the height of a building from a distance or to calculate the angle of elevation to a star.
FAQ Compilation: Unit 7 Homework 2 Special Right Triangles
What are the key characteristics of special right triangles?
Special right triangles possess specific angle measures and side length ratios that distinguish them from ordinary right triangles.
How is the Pythagorean theorem related to special right triangles?
The Pythagorean theorem provides a fundamental relationship between the side lengths of special right triangles, allowing us to determine unknown side lengths.
What are some practical applications of special right triangles?
Special right triangles find applications in architecture, engineering, and other fields where precise measurements and calculations are crucial.