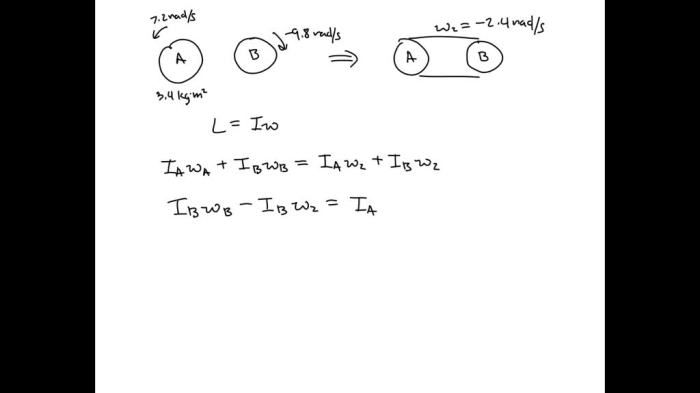
Two disks are rotating about the same axis – Two disks rotating about the same axis is a captivating topic that delves into the dynamics and principles of rotational motion. This comprehensive analysis explores the forces, equations, and energy considerations associated with such systems, providing a thorough understanding of their behavior and applications.
From the basic principles of angular velocity and acceleration to the advanced concepts of gyroscopic motion, this discourse unravels the complexities of rotating disks, shedding light on their significance in various real-world scenarios.
Basic Principles
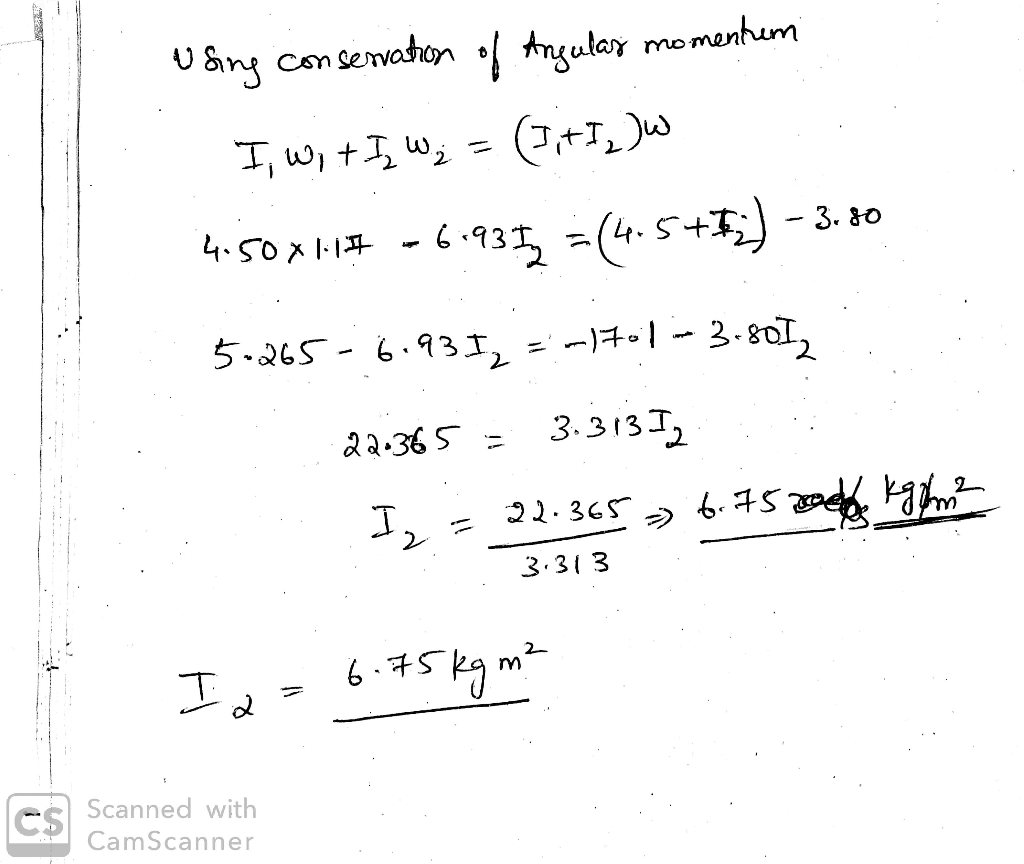
Rotational motion describes the movement of an object around a fixed axis. It involves two key concepts: angular velocity and angular acceleration.
Angular velocity (ω) measures the rate of rotation in radians per second (rad/s), while angular acceleration (α) measures the change in angular velocity over time in radians per second squared (rad/s²).
Rotational motion is related to linear motion through the radius of rotation. The linear velocity (v) of a point on the rotating object is equal to the product of its angular velocity (ω) and the distance (r) from the axis of rotation: v = ωr.
Dynamics of Two Rotating Disks, Two disks are rotating about the same axis
Consider two disks rotating about the same axis. The forces acting on the disks include the force of gravity, the normal force exerted by the axis, and the frictional force between the disks.
The equations of motion for the disks can be derived using Newton’s second law and the concept of torque. The torque (τ) is defined as the product of force (F) and the lever arm (r): τ = Fr.
The conditions for equilibrium occur when the net torque acting on each disk is zero.
Energy Considerations
The kinetic energy (K) of the disks is given by the formula K = (1/2)Iω², where I is the rotational inertia of the disk.
Rotational inertia is a measure of the disk’s resistance to angular acceleration. It depends on the mass and distribution of mass of the disk.
The conservation of energy principle states that the total energy of the system remains constant, even though it may be transformed from one form to another.
Applications
| Application | Description |
|---|---|
| Flywheels | Store kinetic energy and release it smoothly to provide constant power output. |
| Gears | Transmit motion and torque between shafts. |
| Turbines | Convert the kinetic energy of a fluid into mechanical energy. |
Advanced Concepts
Gyroscopic motion is the motion of a rotating object that experiences a torque due to its angular momentum. This torque causes the object to precess, or wobble, around the axis of rotation.
External torques can cause the disks to accelerate or decelerate, depending on the direction and magnitude of the torque.
“The dynamics of two rotating disks about the same axis involve forces, torques, energy considerations, and applications in various real-world systems.”
Quick FAQs: Two Disks Are Rotating About The Same Axis
What is the relationship between linear and angular motion?
Linear motion and angular motion are interconnected through the concept of rotational velocity. The angular velocity of a rotating object is directly proportional to the linear velocity of a point on its circumference.
How do you calculate the kinetic energy of rotating disks?
The kinetic energy of rotating disks is given by the formula Ek = 1/2 – I – ω^2, where Ek is the kinetic energy, I is the rotational inertia, and ω is the angular velocity.
What is the significance of rotational inertia in rotating systems?
Rotational inertia is a measure of an object’s resistance to changes in its angular velocity. A higher rotational inertia indicates a greater resistance to acceleration or deceleration.