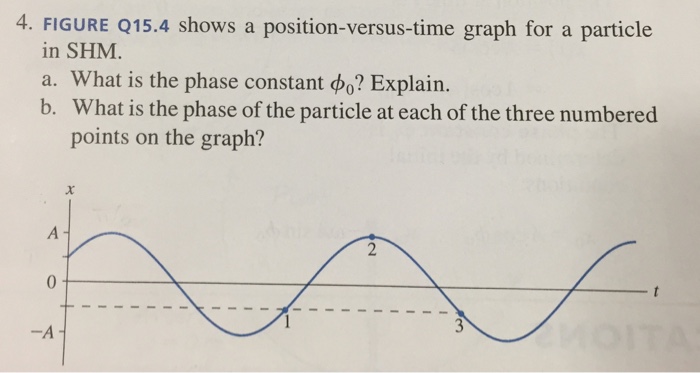
Shows a position-versus-time graph for a particle in shm – The position-versus-time graph for a particle in simple harmonic motion (SHM) provides a powerful tool for understanding the dynamics of this fundamental oscillatory motion. This graph captures the intricate relationship between the particle’s position, velocity, and acceleration, offering insights into the behavior of systems undergoing SHM.
Delving into the intricacies of this graph, we will explore its key features, including amplitude, period, and frequency, and uncover their significance in characterizing the particle’s motion and energy. Furthermore, we will delve into the practical applications of this graph, demonstrating its utility in engineering, physics, and other disciplines.
Basic Concepts of Simple Harmonic Motion (SHM)
Simple Harmonic Motion (SHM) is a periodic motion where an object oscillates back and forth around a central point. It is characterized by a sinusoidal displacement function that repeats itself at regular intervals.
Mathematically, SHM is represented by the equation: x(t) = Acos(ωt + φ), where x(t) is the displacement at time t, A is the amplitude, ω is the angular frequency, and φ is the phase angle.
Examples of SHM in real-world applications include the motion of a pendulum, the vibration of a guitar string, and the oscillations of a spring-mass system.
Position-versus-Time Graph for SHM: Shows A Position-versus-time Graph For A Particle In Shm
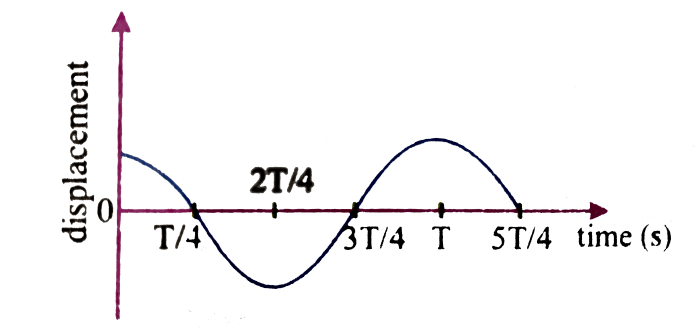
A position-versus-time graph for SHM is a plot of the object’s displacement from the equilibrium position over time. The graph is a sinusoidal curve that repeats itself at regular intervals.
The shape of the graph is determined by the amplitude, period, and frequency of the motion. The amplitude is the maximum displacement from the equilibrium position, the period is the time it takes for one complete oscillation, and the frequency is the number of oscillations per unit time.
Key Features of the Position-versus-Time Graph
- Amplitude:The maximum displacement from the equilibrium position.
- Period:The time it takes for one complete oscillation.
- Frequency:The number of oscillations per unit time.
These features are related to the particle’s motion and energy. The amplitude is proportional to the maximum kinetic energy of the particle, the period is inversely proportional to the frequency, and the frequency is proportional to the square root of the spring constant.
Relationship between Position, Velocity, and Acceleration, Shows a position-versus-time graph for a particle in shm
The position, velocity, and acceleration of a particle in SHM are related by the following equations:
| Position | Velocity | Acceleration |
|---|---|---|
| x(t) = Acos(ωt + φ) | v(t) =
|
a(t) =
|
The graph’s slope represents the velocity, and the graph’s curvature represents the acceleration.
Applications of the Position-versus-Time Graph
The position-versus-time graph for SHM is a useful tool for analyzing and predicting the behavior of systems undergoing SHM. It can be used to determine the amplitude, period, frequency, and other characteristics of the motion.
Applications of the graph include:
- Analyzing the motion of pendulums and other oscillating systems.
- Designing and tuning musical instruments.
- Predicting the behavior of springs and other elastic systems.
Helpful Answers
What is the significance of the amplitude in the position-versus-time graph for SHM?
The amplitude represents the maximum displacement of the particle from its equilibrium position, providing an indication of the energy stored in the system.
How does the period of the graph relate to the particle’s motion?
The period represents the time taken for the particle to complete one full cycle of oscillation, indicating the frequency of the motion.
What is the relationship between the slope of the graph and the particle’s velocity?
The slope of the graph at any point represents the instantaneous velocity of the particle, providing insights into its speed and direction.